LLMs Fight With Both Hands Tied Behind Their Back

We haven't yet given them access to knowledge-in-the-world

So, obviously we need to talk about o3.

(If you’ve been hiding under a rock, or I suppose if you somehow don’t spend every waking minute following AI Twitter: OpenAI recently announced¹ o3, their latest “reasoning” model. It’s not yet available to the public, but they released some astonishing benchmark figures. This included rapid progress on some tasks that had previously been very difficult for AIs, as well as advanced math and programming problems that require elite human-level performance. o3 is the successor to “o1”, itself only a few months old. If you’re wondering what happened to o2, the official answer is that a British telecom company owns the trademark, but I’m confident the real reason is the well-known fact that AI developers have an aversion to logical or even comprehensible names for anything.)

Some early analysis of o3’s capabilities shines new light on the strengths and weaknesses of LLMs², and where things might go from here. In particular, it’s dawning on me that we live in a world designed to support human cognition, full of tools optimized to help meatbrains think. Most of these tools are not available to LLMs (or well designed to work with them. Which raises a new question: what happens when we start giving AIs a toolkit as rich as the one we give ourselves?

To set the stage for that question, I’ll first review o3’s impressive performance on math, programming, and visual reasoning tasks.

FrontierMath: For When the Olympiad Is Too Easy

FrontierMath is a recently announced set of extremely difficult math questions:

FrontierMath is a benchmark of hundreds of original mathematics problems spanning the breadth of modern mathematical research. These range from computationally intensive problems in number theory and real analysis to abstract questions in algebraic geometry and category theory. We developed it through collaboration with over 60 mathematicians from leading institutions, including professors, IMO question writers, and Fields medalists.

FrontierMath problems typically demand hours or even days for specialist mathematicians to solve. The following Fields Medalists shared their impressions after reviewing some of the research-level problems in the benchmark:

“These are extremely challenging. I think that in the near term basically the only way to solve them, short of having a real domain expert in the area, is by a combination of a semi-expert like a graduate student in a related field, maybe paired with some combination of a modern AI and lots of other algebra packages…” —Terence Tao, Fields Medal (2006)

“[The questions I looked at] were all not really in my area and all looked like things I had no idea how to solve…they appear to be at a different level of difficulty from IMO problems.” — Timothy Gowers, Fields Medal (2006)

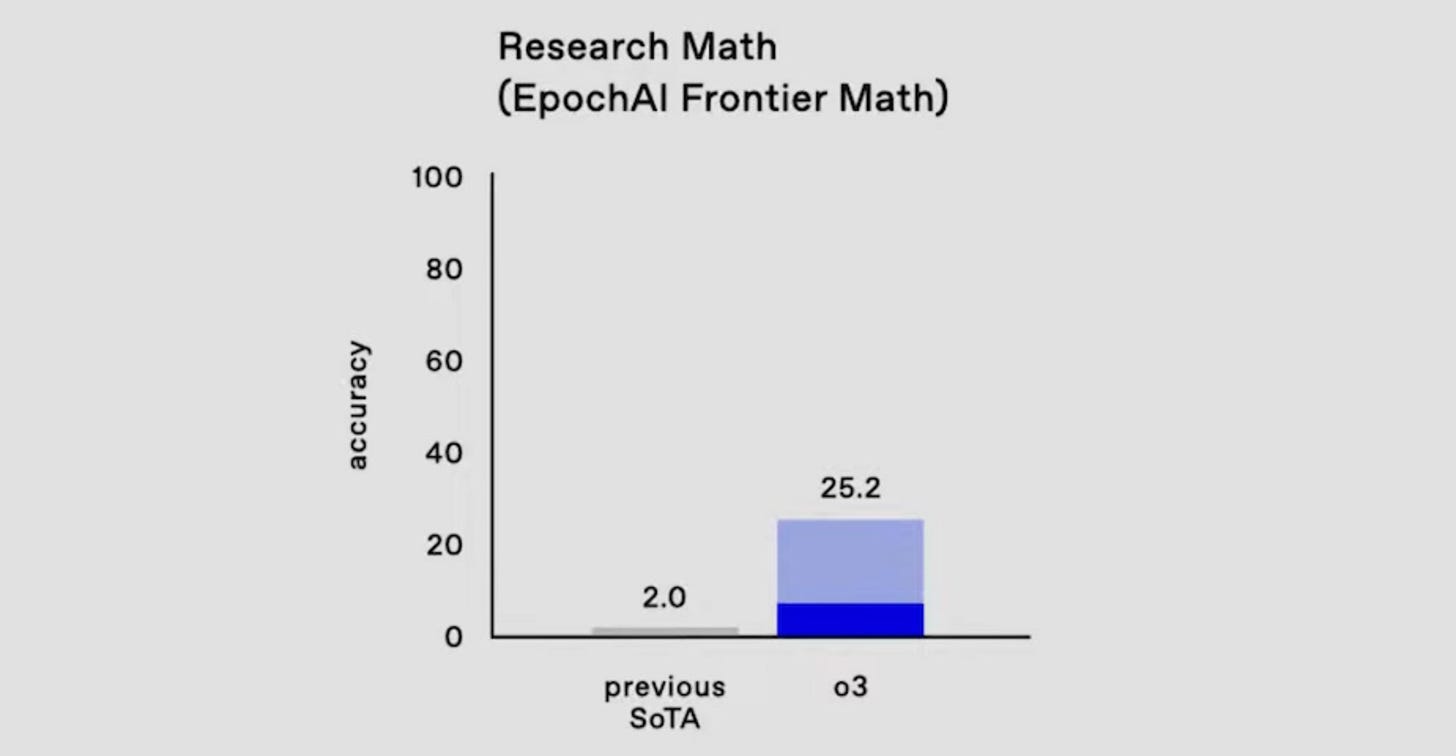
I’ve seen it reported that roughly 25% of the problems are of similar difficulty to the International Mathematical Olympiad (see my September post What It’s Like To Solve a Math Olympiad Problem), and those are the easy ones; they go up steeply from there. Until recently, the highest score reported for any AI system on this benchmark was 2%³. o3 improved this score by a factor of 12:

The teeny little gray bar represents the previous state of the art (SoTA). The dark blue bar is o3’s performance in “low compute” mode, and the light blue is “high compute” mode. My understanding is that in low-compute mode, o3 tries each problem 6 times and attempts to discern the best result; in high-compute mode, it takes the best of 1000 attempts. High-compute mode is obviously expensive, potentially running to thousands of dollars to solve a single problem. But for a difficult or important problem, that can be worthwhile, and costs are sure to plummet.

I was competitive at the international level in the Math Olympiad, but I can’t make head nor tail of FrontierMath problems. A recent Twitter thread by Epoch AI mathematician Elliot Glazer helped me to better appreciate what FrontierMath measures. The thread is worth reading in its entirety, but one critical thing I learned is that each FrontierMath problem is classified on three dimensions:

• Background – how much background knowledge of mathematics is needed? This ranges from general knowledge appropriate to an advanced high school student (like the Olympiad) up to “research level” (specialized knowledge beyond what a graduate student would be expected to have learned).

• Creativity: “estimated as the number of hours an expert would need to identify the key ideas for solving the problem”. This gets at the degree of exploration and insight required to unlock a solution.

• Execution: “estimated as the number of hours required to compute the final answer once the key ideas are found”. Basically, how many steps are required to grind out the answer. Note that the more steps required, the more important it is that each step be error-free.

This is a very helpful mental framework for evaluating the difficulty of a cognitive task in any domain, not just mathematics. LLMs have been superhuman in their breadth and depth of background knowledge since the original release of GPT-4. And OpenAI’s o1 model already demonstrated strong ability at error-free “execution” across a long sequence of steps. For math problems, the remaining barrier has been creativity – coming up with a set of non-obvious insights that allow a problem to be reduced to a set of straightforward steps (execution) requiring only background knowledge.

Glazer reports:

So far, of the problems we’ve seen models solve, about 40% have been Tier 1, 50% Tier 2, and 10% Tier 3. However, most Tier 3 “solutions”—and many Tier 2 ones—stem from heuristic shortcuts rather than genuine mathematical understanding.

I’m not quite sure what he means by this (I asked, but haven’t heard back). But my guess is that o3’s extremely impressive 25% score on FrontierMath is being accomplished without much use of “creativity” or insight. It may turn out that a quarter of the problems are less difficult than intended, if you happen to have learned an enormous number of mathematical facts and tricks and are given 1000 tries to stumble onto one that applies to the problem.

(More commentary on o3’s FrontierMath performance, from a research mathematician, here.)

o3 Prepares to Ruin Programming Contests

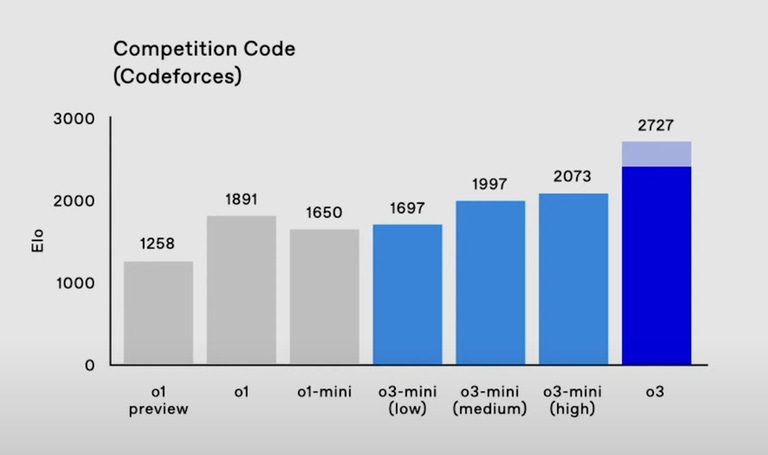
Codeforces is a popular competitive programming platform. Surprise, o3 posted a record score for an AI:

This score would place o3 (in “high compute” mode) at a very elite level – in the top 200 of all human competitors worldwide.

(As one blogger noted, this means that it may soon become impossible to hold serious competitive programming contests online; it will be too easy to cheat by asking an AI for assistance⁴. Of course people will still be able to do this sort of thing for fun, just as people still play chess for fun.)

From 2003-2005, I competed on a similar platform called TopCoder. I briefly reached #3 in the global rankings, and took fourth place at the 2004 annual TopCoder Open. My experience is that TopCoder problems are generally easier than Math Olympiad problems on the “background” and “creativity” scales, but often harder on “execution”. The hardest problems can also require substantial creativity. I took a quick look at half a dozen Codeforces problems, and they seem to be more mathematical in nature than I remember from TopCoder, probably putting more weight on creativity and less on execution. (I asked Claude about this and it rendered a similar opinion.) But as we’ve seen again and again in the last couple of years, an LLM’s superhuman level of background knowledge can often substitute to some extent for creativity – as I said in my very first post on AI, GPT-4 Doesn't Figure Things Out, It Already Knows Them.

Interestingly, while o3 in high compute mode gives elite performance at both FrontierMath and Codeforces, it’s difficult to compare these results to one another. FrontierMath problems require specialist knowledge from specific sub-domains of mathematics, so I presume even a research mathematician would struggle with these problems unless they fell into their particular area of specialization. (The Timothy Gowers quote supports this.) Codeforces problems are more generalist, and I presume that any given top human competitor can solve most of them. Thus a 25% score on FrontierMath might be more impressive, in human terms, than what I presume was a much higher pass rate on Codeforces problems.

ARC: Little Pixel Images are Humanity’s Last Stand

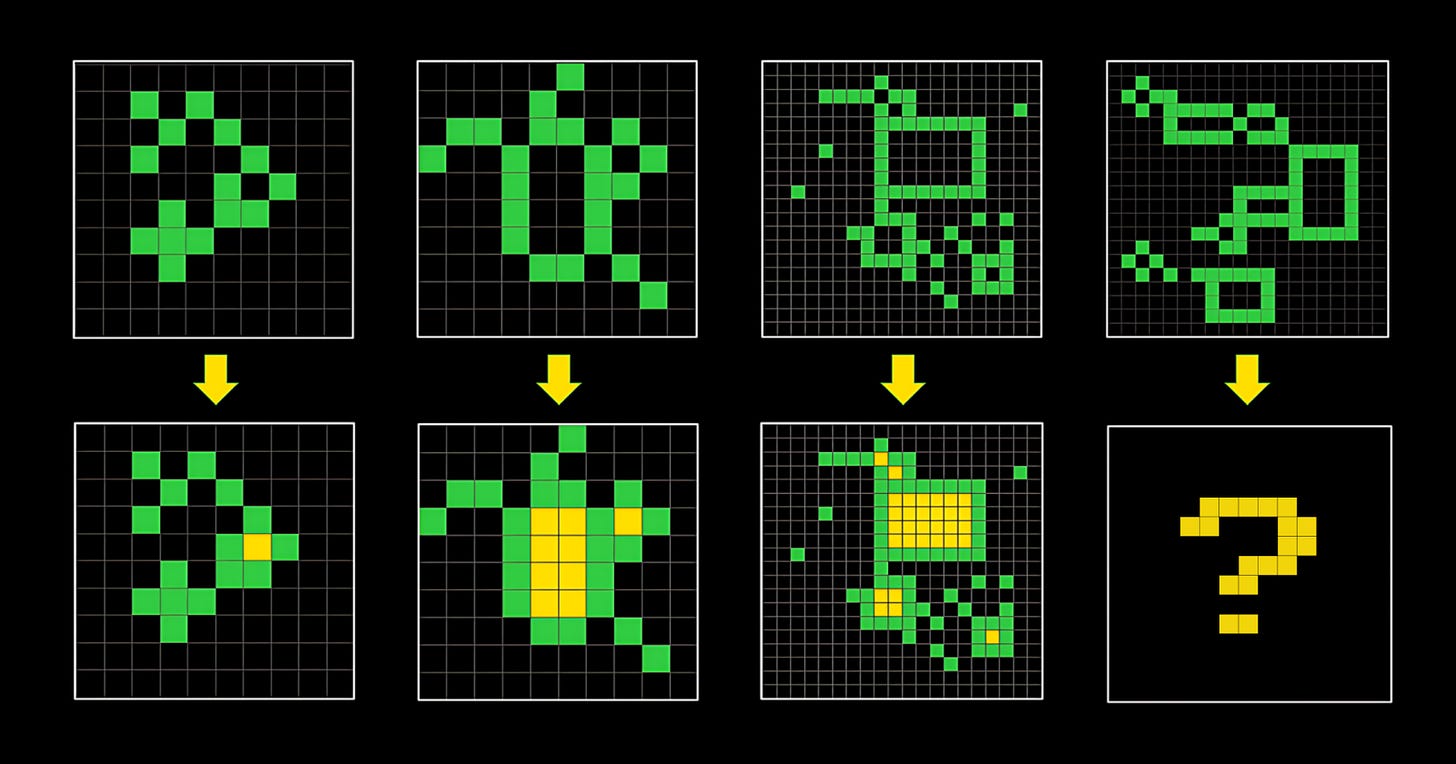
We’ve discussed o3’s performance on math and coding tasks. On to visual reasoning. ARC, or technically ARC-AGI (“Abstract and Reasoning Corpus for Artificial General Intelligence), is a set of visual analogy puzzles. Here’s an example:

In this problem, we’re given three input / output pairs of images, and then a fourth input (in the upper right). The task is to figure out what belongs in the lower-right box. From examining the first three pairs, we can see that the rule is to fill in all of the fully-enclosed areas in yellow.

If you’d like to try some of the problems yourself, go to arcprize.org/play. They’re kind of fun, and mostly not too difficult, although clicking on each little square to build the answer image can be very tedious.

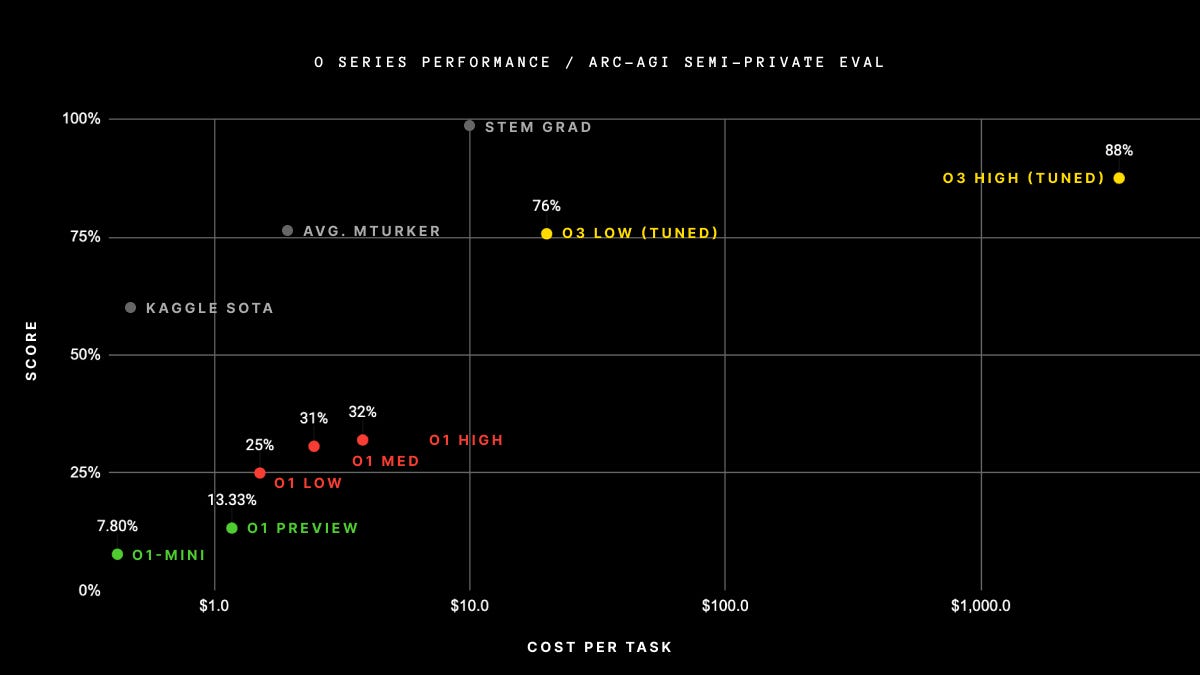
The ARC challenge was first published in 2019, and for some years after there were no AI solutions that could solve a significant fraction of the problems. Scores began climbing over the course of 2024, but – you guessed it – o3 blows previous contenders out of the water:

In this graph, “Kaggle SOTA” was, if I understand correctly, the previous best score for an AI, at around 60%. o3 in the “low compute” variant scored 76%, just below the average for humans on Amazon’s Mechanical Turk platform, and o3 in the “high compute” variant scored a remarkable 88%.

It’s interesting that o3’s ARC score, while very impressive as a technical accomplishment, is only moderately better than the average performance of indifferently-motivated human workers. On the math and coding benchmarks, by contrast, o3 was strongly competitive with elite human performers giving their best effort. In other words, relative to human performance, o3 is far less impressive at ARC than at math or coding problems. I’ll come back to this idea in a minute.

(Regarding the challenge level of ARC problems: I tried a dozen questions myself and found them pretty easy. I solved all 12, and in most cases I figured out the rule in just 5-10 seconds⁵. The “semi-private eval” problems being scored here are more difficult than the problems available to the public, but o3 high compute only scored 92% on the public test set, and I’m pretty sure many people could beat that.)

It’s worth noting that using o3 to solve these problems is expensive: on the public test set, $17 per problem for o3-low-compute, and about $2900 per problem (!) for o3-high-compute. Again, by contrast, I found that I could generally get the key idea for these problems in 5-10 seconds. It then takes another minute or two to click all the little boxes, but that is peripheral to the intelligence question that ARC is intended to measure, and would be greatly reduced with a small amount of work on the app (e.g. allowing click-and-drag to fill in multiple pixels at once).

Of course these costs will come down rapidly: LLM operation costs have been declining at about 10x per year. I’ll discuss the implications of that later.

Why o3 Struggles at ARC

I was moved to write this post after coming across a fascinating analysis of o3’s ARC-AGI struggles by Mikel Bober-Irizar: LLMs struggle with perception, not reasoning, in ARC-AGI. He points out that LLMs like o3 are primarily designed to handle textual input, not pixel images⁶. Apparently, OpenAI presents ARC problems to o3 in textual format, using a digit to represent each pixel. For example:

Find the common rule that maps an input grid to an output grid, given the examples below.

Example 1:

Input:
0 0 0 5 0
0 5 0 0 0
0 0 0 0 0
...

However, LLMs don’t really “see” formatting the way we do. They see text as a linear sequence. So each image in the problem statement is presented to o3 as a one-dimensional blob:

Find the common rule that maps an input grid to an output grid, given the examples below.

Example 1:

Input: 0 2 0 0 0 2 5 2 2 0 5 2 5 5 0 2 2 5 2 2 5 5 0 2 0 0 2 ...

(For a complete example, see here.)

Obviously, o3 will have a difficult job in observing and reasoning about two-dimensional patterns when the images are presented this way. It will need to reconstruct the spatial relationships “in its head”. And Mikel notes plenty of evidence that o3 is struggling with the basic spatial nature of the problems, rather than the abstract reasoning that ARC-AGI is intended to measure. For one thing, o3 (and other LLMs) have more difficulty with ARC problems as the pixel grid gets larger, meaning that there are more rows and columns to keep track of. Humans, by contrast, show similar scores on problems of any size. For another, when o3 gets an ARC problem wrong, as Mikel says, it “clearly ‘had the right idea’ but failed to output a correctly sized grid or skipped a row”. Here’s an example:

The grey section shows the examples given in an ARC problem. The green section shows o3’s two attempts to solve it, and the… um… beige? section on the right shows the correct solution. As Mikel says, o3 clearly had the right idea… but it garbled the pixel arrangement in a way that would never happen if it could properly perceive 2d structures.

This gives us a clear explanation for why o3’s performance on the ARC-AGI test is comparatively much less impressive than its performance on math and coding tests: o3, like other LLMs, is missing an important toolkit for reasoning about 2D images.

Once you start thinking about the handicap LLMs labor under when working on ARC-AGI problems, you realize that LLMs are handicapped for many other sorts of tasks as well.

LLMs Live in a World Designed for Humans

When you hand a task to an LLM, it reads the description one word⁷ at a time, and then it thinks out its answer one word at a time. It can’t go back and re-read the problem description, nor can it re-read its own work in progress. Its only access to any of the information it has previously encountered or generated is through its internal memory. Technically known as a “KV cache”, this is a mathematical data structure that contains the model’s processed interpretation of the input text, not the raw words. Furthermore, the model can only retrieve information via a fuzzy mathematical operation that evolves naturally over the course of the model’s training. If you are working on an ARC problem, and you want to check exactly how many red pixels were in the third row of the second example, you can go and look. The best the LLM can do is to try to retrieve that information from its fuzzy mathematical memory.

Imagine that you’ve been asked to summarize a scientific paper. If you read a sentence like “Image 3 shows several examples of propagating fractures”, you can shift your eye to the image, study it until you identify the fractures, and then resume reading. An LLM can’t control the order in which information is presented to it, so it will need to hold that thought until it comes to the image. If it has already passed the image, and it didn’t pay attention to the fractures, it can’t go back now to look for them.

When presented with a paper, some readers might like to skip ahead and review the conclusions first. They might skim the entire paper and then re-read it more carefully. As they read, they might choose to stop and Google a term, or flip back to review an earlier point, or scribble a few calculations to check their understanding. Certainly they might want to take notes as they proceed. An LLM can’t do any of these things. A “reasoning model” like o3 can make intermediate notes to itself, but only after being force-fed the input data; it can’t control the order in which the inputs are presented, or make notes while ingesting them.

Now imagine a software engineer assigned the task of modifying a large program. They will likely be working with a highly sophisticated tool known as an “integrated development environment”, or IDE. One of the most popular, IntelliJ, is developed by a team of over 600 people. An IntelliJ user can jump back and forth through the code. When they see the name of a subroutine, a single click will reveal where that subroutine is defined, or all the places it is used. If they want to give that subroutine a new name, the IDE will make the change everywhere the name is referenced. The “debugger” allows the engineer to watch the program execute; other tools flag common mistakes, or allow complex restructurings to be performed with a few clicks.

Now imagine you assign the same task to an LLM. It can’t use an IDE, so you’ll have to present it with the full text of the program, possibly consisting of many files. The LLM is forced to read through each file from beginning to end, in the order you presented them, and it can never go back to re-read. It can’t navigate through the code, or watch the program execute, or rely on any other other capabilities developed by IntelliJ’s engineering team over the course of decades. It can only rely on the information stored in its head.

Knowledge In the Head vs. Knowledge In the World

I first encountered the concept of “knowledge in the world” in Don Norman’s classic book The Design of Everyday Things. It represents the idea that much of the information we need to get through our day can be obtained on demand from things around us, rather than needing to reside in our heads.

We make such natural use of knowledge-in-the-world that we often fail to even recognize that we are doing so. To navigate out my front door, I don’t need to remember its exact location, or that the handle needs to be depressed rather than twisted; once I emerge from the kitchen, I can see the door and the handle. As I write this blog post, if I think of an idea that I’d like to incorporate into the opening paragraph, I don’t need to remember exactly how that paragraph is currently phrased; I can scroll up and look at it.

LLMs can’t use knowledge in the world, because we haven’t connected them to the world. They can’t scroll back and re-read the first paragraph of an essay they are writing.

Knowledge in the world is such a powerful concept that we need to reassess all of our views on LLM capabilities in light of the fact that they are getting by without it.

AI Has Been Operating Under a Handicap

The accomplishments of o3 and other LLMs are even more impressive when you realize just how thoroughly we rely on the knowledge-in-the-world that they can’t access.

Actually, it’s not quite true that LLMs can’t access external knowledge. Some LLM-based systems, such as ChatGPT, incorporate “tool use” – a mechanism that allows the LLM to do things like perform a Google search or write and run small computer programs. However, this has not been extended to fine-grained interactions such as managing a todo list, organizing a set of notes, or reviewing particular pieces of input or output data. o3, while tackling a FrontierMath problem, can’t draw itself a diagram; while working on an ARC puzzle, it can’t look at the image sideways.

We may soon find ways of extending tool use to incorporate more of the little moment-to-moment actions we take to bring the right information into our brains at the right time. When that happens, it may yield another big jump in AI capabilities. Our entire world – the way we present information in scientific papers, the way we organize the workplace, website layouts, software design – is optimized to support human cognition. There will be some movement in the direction of making the world more accessible to AI. But the big leverage will be in making AI more able to interact with the world as it exists.

We need to interpret LLM accomplishments to date in light of the fact that they have been laboring under a handicap. This helps explain the famously “jagged” nature of AI capabilities: it’s not surprising that LLMs struggle with tasks, such as ARC puzzles, that don’t fit well with a linear thought process. In any case, we will probably find ways of removing this handicap. In his controversial paper Situational Awareness, Leopold Aschenbrenner forecast rapid advances based in part on the potential for “unhobbling” the models. I’m not sure this is the form of “unhobbling” he had in mind, but we should factor it into our thinking.

Giving LLMs access to knowledge-in-the-world will compound with other ongoing advances, such as the 10x-per-year cost reduction that I mentioned earlier. By the end of 2028, it might cost a dime to perform a task that currently costs $1000 using o3 – before taking into account any efficiency gains that might allow LLMs to get more done with less thinking, for instance by incorporating knowledge-in-the-world.

Does this mean that the singularity is upon us, after all? Not necessarily. As I wrote last month, AI is racing forward but the destination could still be a long way off. Or maybe not! Isn’t profound uncertainty fun? In an upcoming post, I’ll speculate as to the path from here to AGI.

1. I would link to the announcement, but annoyingly, the best I can do is tell you to go to https://openai.com/12-days/ and play the video near the top of the page – find the big picture with three people sitting around a table and click the Play button in the lower-left corner.

2. Large Language Models – the term for the sort of AI used in tools like ChatGPT.

3. So far as I’m aware, Google’s AlphaProof system – which achieved strong performance on this year’s IMO problem set – has not been tested on FrontierMath. AlphaProof does require human assistance to translate problems into a formal language, which might disqualify it.

4. Out of curiosity, I asked Claude what impact chess programs have had on online competitive chess. Apparently online chess platforms have developed robust anti-cheating methods, looking for signals such as unnatural patterns of mouse movement, unnatural consistency in thinking time, “performance in complex positions vs tactical position”, and “play during crucial moments (humans tend to make more mistakes under pressure)”. I find myself uncertain as to whether similar measures could be developed for programming competitions. People are clever, but that applies to the people on both sides of the problem.

5. For one of the problems, I needed two tries to get the right answer, but I believe the formal rules of the ARC test allow for two tries, and in any case it was a silly mistake that I would not have made if I’d had a clearer understanding of how the test is intended to work – this happened on only the second problem I tried.

6. While it’s true that many newer LLMs are “multimodal” and can handle other forms of input, such as images or audio, o3 was given the ARC problems in textual format, not as images. I’m not sure why. Some possibilities: o3 may not be a multi-modal model; its reasoning capabilities may not not have been trained on images; its image training set may not have included low-resolution “pixel art” images (my understanding is that multimodal LLMs in general struggle with such images).

7. Yes, I’m conflating “words” with “tokens”. If you don’t know the difference, don’t worry about it. If you do know the difference, also don’t worry about it.