Learning to Explore: AlphaProof and o1 Show The Path to AI Creativity

An Impressive Start, But Many Hurdles Lie Ahead

LLMs¹ and other models can generate pretty much anything: scientific papers, business plans, architectural drawings, movie scenes. But in some cases, inspection will reveal the results to be nonsense. A TV script generated by an LLM will be like late-season Game of Thrones: all the right elements are there, but they’re thrown together haphazardly, and the result doesn’t really work.

In my last post, I argued that the frontier of AI capabilities is now defined by the set of tasks for which AIs can generate results that stand up to scrutiny. Recently, Google’s AlphaProof and OpenAI’s o1 have extended this frontier, using new training techniques to solve math, science, and coding problems for which previous models would have generated plausible-looking gibberish.

This is revealing: if simple scaling were all that was necessary to advance AI capabilities, then these companies would be laser focused on building GPT-5 and Gemini 2. The approaches they used for AlphaProof and o1 reveal important insights into the path to AGI.

Creativity is an Exploratory Process

Let’s begin by reviewing the core mechanism of human creativity. As an example of how people go about solving difficult problems, I recently worked through a problem from the latest International Mathematical Olympiad, and wrote a detailed explanation of my thought process. Here’s a summary of my path to the solution. Don’t bother following this, just note how convoluted it is:

1. Break the problem down into pieces.

2. Re-read each piece until I fully understand it.

3. Work through a simple example.

4. Identify a pattern.

5. Find an explanation for the pattern.

6. Try to prove that this pattern will always hold…

7. …but eventually decide that it’s hopeless.

8. Work through more examples; discover that the initial pattern did not always hold.

9. Notice some more general patterns, and prove that they always hold.

10. Pursue an idea for completing the proof…

11. …and then abandon it.

12. Come up with a new way of representing the data in the problem.

13. Using this representation, notice that a standard proof technique might apply…

14. …but fail to make it work.

15. Identify another potentially applicable proof technique.

16. Notice a roadblock…

17. …and find a change of representation that resolves it.

18. Notice another roadblock…

19. …and find another change of representation.

20. Success!

Note that I did not begin with any sort of plan. Tasks requiring true creativity resist planning. In this case, the crucial idea did not emerge until I was nearly done. Until that point, I was mostly just wandering around, looking for opportunities to chip away at the problem.

I think most creative work is like this. As we work, we learn more about the problem, forcing us to constantly replan. We have more expressions to describe this sort of thing than the Inuit have for snow: “The creative process”, “brainstorming”, “wrestling with the problem”, “playing with an idea”, “fleshing it out”, “it’s still half-baked”, “exploring solutions”, “taking a step back”, “sleeping on it”, “working out a few kinks”, “tearing up the plan and starting over”.

If we want computers to undertake creative problem solving, we will need to teach them how to explore.

Effective Exploration Is Its Own Skill

The creative process may be unplanned, but it is not haphazard.

To solve the Olympiad problem, I relied on a collection of hard-won strategies for math problems: play with examples, look for patterns. If you can’t prove something is true, look for a counter-example. Assign shorthand names to important ideas.

To effectively apply a strategy, you need muscle memory: an intuitive sense for which strategies to try in a given situation, and how to adapt a strategy to specific circumstances. This comes from having used the strategy in multiple contexts. It’s not enough to have read about it in a textbook.

I think most creative work relies on a similar collection of strategies. This is a completely different kind of knowledge from what LLMs understand today. AGI will require developing models that can learn and employ these strategies.

LLMs Can Apply Techniques, But Not Strategies

Current LLMs have mastered a wide range of techniques and structures. They can use a metaphor; they can construct a proof by contradiction; they can write a transition sentence.

But they aren’t very good at following strategies. If you ask ChatGPT to write an essay, it will just start writing. It won’t take time to think through a thesis². It won’t realize, halfway through, that the paragraph it’s about to write would flow better if it could add a sentence to the introduction. It won’t pause to research some supporting material for a point it’s about to make.

If you ask it to write a proof, again, it’ll just dive in. It won’t work through a few examples to get started, or play around to see which proof technique can be made to apply.

You can tell it to do those things, but it won’t do them very well, because it’s never learned how. A while back, I wrote an entire post explaining that we train LLMs on finished essays, but not on the editing process; on working code, but not the art of debugging. AI models struggle with activities that don’t arise in their training data. In a recent post, Timothy Lee cites the example of a model which was trained to drive a video game car by learning from expert human players. Because the experts never made mistakes, the AI didn’t learn how to recover from mistakes, and then:

…once in a while, the AI would make a small mistake—say, swerving a bit too far to the right. Then it would be in a situation that was a bit different from its training data. That would make it more likely to make another error—like continuing even further to the right. This would take the vehicle even further away from the distribution of training examples. So errors tended to snowball until the vehicle veered off the road altogether.

Just as the video game AI never learned to recover from mistakes, LLMs aren’t taught strategies for creative exploration. People have tried to address the failure of LLMs to apply strategies by building systems that explicitly prompt them to do so: “think step by step”, “break down the problem into pieces”, “rewrite this draft”. In his Situational Awareness paper, Leopold Aschenbrenner calls this “unhobbling” and argues that such techniques will support rapid progress toward AGI:

Rather than just asking a model to solve a problem, have one model make a plan of attack, have another propose a bunch of possible solutions, have another critique it, and so on.

However, such an approach can’t get away from two basic facts:

1. Even if we tell an LLM to apply problem-solving strategies, traditional LLMs won’t do it very well, because they weren’t trained for it³.

2. Sophisticated problem solving requires fluidly jumping from one strategy to another. LLMs are good at that sort of fluidity when they’re given a rich variety of training data. But we don’t train LLMs to choose strategies, and if we simply tell them which strategy to use, there’s no fluidity at all.

Because LLMs are trained on finished work, teaching AIs to make effective use of exploratory strategies will require a new approach. Let’s look at a couple of recent attempts.

Enter AlphaProof

In July, Google DeepMind announced AlphaProof, an AI system that can tackle exactly the sort of creative task that I’ve been arguing is difficult for standard LLMs. In conjunction with a similar system called AlphaGeometry, it solved four of the six problems on this year’s International Math Olympiad – better than all but the very top human competitors.

Google has not said much about how AlphaProof works. My understanding is as follows: when presented with a problem, it attempts to simply write out a proof, using a language model trained on millions of proofs⁴. It sounds like it may use a tree-search approach, similar to chess AIs. That means it would pick a few promising candidates for the first step of the proof; for each of those, it would try a few continuations, and then several continuations to each of those continuations, and so forth. It continues exploring possibilities until it finds a valid proof – potentially trying millions (billions?) of paths along the way.

This is very different from the strategies that people employ to solve math problems. There’s no room for the model to play with the problem, look for patterns and try to explain them, assign shorthand names to important concepts, or work forwards and backwards. However, just as chess AIs are able to explore far more continuations than a human grandmaster, AlphaProof can explore a superhuman number of potential solutions.

Interestingly, AlphaProof does employ one trick that might help compensate for its lack of deliberate exploration. It will automatically generate simplified versions of a problem, attempt to solve those, and then fine-tune itself on successful proofs. In this fashion, it may manage to learn more about the original problem and how to solve it.

As an example of the difference between the human and AlphaProof approaches, consider problem 1 from this year’s IMO⁵. It asks us to determine which real numbers satisfy a certain property. It turns out that the answer is “all even integers”. By playing around with the problem, it’s not too difficult for someone with the right math background to guess that this is the answer – I got there in a few minutes. Then you can focus on the real challenge: proving it.

According to Jonathan Paulson, AlphaProof took a more brute-force approach. It “generated several hundred guesses” as to which numbers have the specified property, and then “ruled lots of them out by finding simple counterexamples before ending up with a small shortlist that it then worked on⁶”. Trying out hundreds of guesses is much less efficient than playing with the problem and intuiting the correct answer. As Paulson later noted:

…human guesses are structured differently. We often reach the right guess by starting with a wrong guess, seeing why it is wrong, adjusting it, seeing why the adjustment is wrong, adjusting it again, etc.

With regard to AlphaProof’s overall work on the 2024 IMO, Paulson adds:

The main qualification is that the program needed a lot longer than the human competitors – for some of the problems over 60 hours – and of course much faster processing speed than the poor old human brain.

There is a lot we don’t know about AlphaProof: how exactly does it work? How much processing power did it use? Will it generalize to other problem domains, or to more complex or difficult math problems? But we do know that on crisply specified mathematical problems, it performs at the level of elite high school students – an impressive advance in AI capabilities, even if it relies on a substantial application of brute force.

Next, let’s look at the new model from OpenAI that has been generating so much buzz.

o1

Here is how OpenAI describes o1:

We've developed a new series of AI models designed to spend more time thinking before they respond. They can reason through complex tasks and solve harder problems than previous models in science, coding, and math.

OpenAI has not yet released the full o1 model. We currently have access to “o1-mini” (a smaller, less capable version), and “o1-preview” (an incomplete version of the full model).

For some tasks, o1, and even o1-mini and o1-preview, are much more capable than any previous LLM. Cue the impressive graphs⁷:

Here’s a sample problem, provided by OpenAI, which o1-preview solves correctly:

oyfjdnisdr rtqwainr acxz mynzbhhx -> Think step by step

Use the example above to decode:

oyekaijzdf aaptcg suaokybhai ouow aqht mynznvaatzacdfoulxxz

(The first line is showing an example of a code; the task is to figure out the code and apply it to the last line.) I’ll put the answer in a footnote, in case you want to try the problem yourself⁸. It’s not super difficult, but I find it quite impressive that o1 was able to both figure out the code, and correctly decode the entire message without any important mistakes.

For a practical example, Ethan Mollick shares a snippet from a writeup by a healthcare startup:

We tested o1-preview’s ability to determine the cost for a newborn delivery. o1-preview demonstrated a breakthrough at determining costs by correctly identifying relevant rules to apply from a contract, making assumptions where needed, and performing calculations. We were particularly impressed by its ability to identify nuances such as special carve outs for high-cost drugs that the mother had to take, apply compounding cost increases, and explain cost discrepancies due to secondary insurance plans and the mother’s complications including a UTI. Most notably, it independently applied this logic without specific prompting.

While o1 is quite impressive, it has limits. In one of my first experiments, o1-preview made mistakes on a straightforward math puzzle based on the short-lived New York Times “Digits” game⁹. o1 also shares some of the foibles of the older models it’s based on. People love to point out that if you ask an LLM a question which is easy, but resembles a classic harder puzzle, the LLM will answer the classic puzzle instead. Julius Simonelli provides an example of o1-preview making the same mistake.

Alex Lawsen gives some helpful perspective:

o1 is absurdly superhuman at some things and absurdly subhuman at some things. The same was true for previous models. If all you do is look for extreme examples in either direction, you will learn no more than that they exist.

Finally, here’s an assessment from famed mathematician Terence Tao:

…the results were better than previous models, but still slightly disappointing: the new model could work its way to a correct (and well-written) solution *if* provided a lot of hints and prodding, but did not generate the key conceptual ideas on its own, and did make some non-trivial mistakes. The experience seemed roughly on par with trying to advise a mediocre, but not completely incompetent, graduate student.

Considering where things stood just a couple of years ago, “mediocre, but not completely incompetent, graduate student” is extremely impressive! But, also, mediocre. As Sam Altman himself said:

o1 is still flawed, still limited, and it still seems more impressive on first use than it does after you spend more time with it.

In summary, o1 has serious limitations, but is still a major practical advance. I expect economically valuable applications to appear quickly, and I’m looking forward to using it as a coding assistant. (For a few more selected takes on o1, see this footnote¹⁰.)

To understand what o1 tells us about the path to AGI, let’s explore what we know about how it works.

Thinking Step By Step By Step By Step By Step

Better finish soon, he’s almost out of paper

The consensus seems to be that o1 is neither “smarter” nor more “knowledgeable” than previous LLMs. The best guess seems to be that o1 is a version of ChatGPT¹¹ that has been fine-tuned to be able to guide itself through an extended reasoning chain. Like earlier LLMs, it still generates output one token at a time, but now that output can include a long series of reasoning steps before arriving at a final product. It’s capable of chewing on a problem for several minutes, during which its chain of thought may extend for many thousands of words, and it is much less likely than previous LLMs to forget details or commit logic errors. As OpenAI explains:

Similar to how a human may think for a long time before responding to a difficult question, o1 uses a chain of thought when attempting to solve a problem. Through reinforcement learning, o1 learns to hone its chain of thought and refine the strategies it uses. It learns to recognize and correct its mistakes. It learns to break down tricky steps into simpler ones. It learns to try a different approach when the current one isn’t working. This process dramatically improves the model’s ability to reason.

OpenAI published chain-of-thought transcripts for a handful of problems¹². They make for illuminating reading. None of the examples show use of any complex problem-solving strategies. Like AlphaProof, o1 never assigns shorthand names to important concepts, or works forwards and backwards. It never says things like “I now understand that the central challenge is X, so let’s consider techniques that are known to handle X”. Everything that o1 accomplishes, it accomplishes through a mundane and extended grind. Each step is something that gpt-4o and its peers were already capable of, but were not able to reliably chain together at this length.

o1’s reasoning traces are often quite verbose. Here’s a snippet from it solving the decoding problem I mentioned earlier – the full trace is much longer:

Given the time constraints, perhaps the easiest way is to try to see patterns.

Option 1: Try to find mapping from letters to letters.

Do any letters match?

First, let's write down the ciphertext and plaintext letters on top of each other.

Ciphertext: o y f j d n i s d r r t q w a i n r a c x z m y n z b h h x

Plaintext: T h i n k s t e p b y s t e p

Wait a minute.

I think maybe there is an anagram or substitution cipher here.

Alternatively, I think that we can notice that each group of ciphertext corresponds to a plaintext word.

Check the number of letters.

First ciphertext word: oyfjdnisdr (10 letters)

First plaintext word: Think (5 letters)

Hmm.

Second ciphertext word: rtqwainr (8 letters)

Second plaintext word: step (4 letters)

Third ciphertext word: acxz (4 letters)

Third plaintext word: by (2 letters)

Fourth ciphertext word: mynzbhhx (8 letters)

Fourth plaintext word: step (4 letters)

Interesting.

It seems that the ciphertext words are exactly twice as long as the plaintext words.

(10 vs 5, 8 vs 4, 4 vs 2, 8 vs 4)

Idea: Maybe we need to take every other letter or rebuild the plaintext from the ciphertext accordingly.

Let's test this theory.

If we take every other letter from the ciphertext words, maybe we'll get the plaintext.

Let's try this for the first word:

Ciphertext word: o y f j d n i s d r (10 letters)

Alternate letters:

First letters (positions 1,3,5,7,9): o f d i d

Second letters (positions 2,4,6,8,10): y j n s r

Wait: Let's try taking every second letter or first letter.

Option 1: Take the odd positions:

Positions: 1 3 5 7 9

Letters: o f d i d

Plaintext word is "Think", letters are T h i n k

Hmm.

Perhaps we can map letters:

o f d i d --> Think

Not directly

Option 2: Try mapping as per an assigned code: perhaps columns of letters?

Alternatively, perhaps the cipher is more complex.

Alternatively, notice that "oyfjdnisdr" has 10 letters and "Think" has 5 letters.

What if each plaintext letter is being represented by two ciphertext letters?

This completes our brief exploration of what AlphaProof and o1 can do, and how they do it. Now we can shed some light on the prospect for AIs to take on a wider variety of creative tasks.

The Race to Capture Chain-of-Thought Data Has Begun

AlphaProof and o1 each represent a substantial advance, but both are limited. AlphaProof can only solve tidy math problems, of a scale that can be solved by (elite) high school students in an hour or two, and only through the use of enormous amounts of computing power. o1 can solve a broader range of science, coding, and math questions, but it can’t handle problems as complex as AlphaProof.

We can presume that neither model was easy to train. For AlphaProof, DeepMind had to generate millions of mathematical proofs. For o1, OpenAI seems to have generated and evaluated a very large number of reasoning transcripts in the specific problem domains o1 is good at¹³.

It’s also worth repeating that neither AlphaProof nor o1 seem to be capable of employing any advanced problem-solving strategies, such as working backwards from the goal. Nor do they seem capable of “thinking about thinking”; o1 will sometimes spontaneously notice that it is stuck and needs to try another path, but it doesn’t seem to be capable of applying higher-level reasoning to reach that conclusion.

I think it’s noteworthy that these limitations correspond closely to the nature of each models’ training data. Nathan Labenz may have hit the nail on the head:

The race to capture chain of thought for everything begins now.

What are the best ways to record the problem solving process?

AlphaProof and o1 can employ the reasoning techniques that appear in their training data, on the problem domains of the training data. This suggests that to further develop AI problem-solving capabilities, we will need to generate more kinds of training data. How hard will that be?

Not All Problems Have a Clear Right Answer

I mentioned that to train AlphaProof, DeepMind generated millions of mathematical proofs. This task was greatly facilitated by the fact that it is easy to tell whether a proof is correct. It’s also relatively easy to generate correct proofs at random, if you don’t care what it is that you wind up proving.

Imagine that DeepMind had, instead, wanted to create an AI that could write short stories, or product designs. I don’t know how they could have generated millions of high-quality examples as training data. It seems like a difficult challenge.

o1 is not limited to mathematics; its extended reasoning capabilities are also reported to extend to science questions and coding tasks. However, these are still domains which have right and wrong answers. I don’t know how OpenAI created o1’s training data, but it seems unlikely to be a coincidence that they targeted domains with well-defined problems and objectively correct answers.

In truth, it is only mathematics where it is always possible to say objectively whether a problem is correct or not. When coding, it’s often difficult to determine whether a program is free of bugs. And even if a program is “correct”, it might not be good; it could be too slow, or overly complicated. Meanwhile, in science, we often have to rely on approximations. This may be why DeepMind developed AlphaProof and not AlphaCoder or AlphaScientist.

Not only is mathematics almost unique in having absolutely clear right and wrong answers; it also tends to have unusually tidy questions. The problem statement for a mathematical theorem is self-contained. The task of planning a marketing campaign, by contrast, depends on a wealth of context regarding the product, brand, target customer, and competitive landscape. The majority of real-world problems have this quality of being difficult to fully characterize in a self-contained problem statement. (For example, programmers generally have to fit their work into a large existing codebase.) As Timothy Lee writes in his analysis of o1, The real world is far messier than math problems.

So the road ahead may be more difficult for areas outside of math and, to a lesser extent, science and programming. What are the prospects for progress within these more objective domains?

IMO Problems Are Impressive, But Aren’t The Endgame

From Zvi:

IMO problems are simultaneously:

1. Far more ‘real math’ than anything you otherwise do as an undergrad.

2. Not at all close to ‘real math’ as practiced by mathematicians.

He then points to a Twitter thread from mathematician Timothy Gowers:

It will be interesting to see how the time the program takes scales as the difficulty of the problems it solves increases. If it scales with a similar ratio to that of a human mathematician, then we might have to get worried.

But if the function [human time taken → computer time taken] grows a lot faster than linearly, then more AI work will be needed. 

The fact that the program takes as long as it does suggests that it hasn't "solved mathematics".

However, what it does is way beyond what a pure brute-force search would be capable of, so there is clearly something interesting going on when it operates. We'll all have to watch this space.

So AlphaProof is already powerful enough to be quite useful, once it’s made more efficient, but also has a long way to go to render human mathematicians obsolete.

Suppose that, to generate a 20-step proof, AlphaProof needs to consider one million possibilities. To generate a 40-step proof, it might need to consider a trillion possibilities (one million squared); for 60 steps, one quintillion possibilities (1,000,000,000,000,000,000). If that’s the way the scaling works, then further progress will require additional breakthroughs.

Those breakthroughs might require generating training data that includes examples of more complex reasoning strategies. Similarly, for o1 to tackle more complex problems, OpenAI might need a way to generate (and grade) millions of examples of reasoning chains that use complex strategies.

This might turn out to be quite difficult. I get the impression that o1 can (sometimes) solve problems that might take a person up to, say, half an hour? But real-world tasks can require days, weeks, or months of effort. Generating training data for those sorts of tasks might be much more difficult and expensive. And we may find that entirely new categories of skill are required, such as the ability to bring relevant data in and out of long-term memory¹⁴. (Probably we can’t even guess at all of the skills that are necessary to manage oneself through a week-long creative project. We won’t recognize what they are until we watch o2 or o3 stumble for lack of those skills.)

With this review, we’re finally ready to say something about the road ahead.

The Long and Winding Road to AGI

AlphaProof and o1 represent impressive advances in AI capabilities. AlphaProof might be too specialized (and expensive?) to have much practical use today, but it has set a new bar for AI problem solving. o1 will find immediate application, which will only increase as people learn how to best use it. And it is certain that further advances will follow. Per Sam Altman¹⁵:

The model (o1) is going to get so much better so fast [...] Maybe this is the GPT-2 moment, we know how to get it to GPT-4. So plan for the model to get rapidly smarter.

My guess is that extending these systems to longer reasoning chains and more complex problem-solving strategies will turn out to be a many-year project. (The journey from GPT-2 to GPT-4 took four years.) It won’t just be a question of scaling up. The fact that o1’s capabilities are specific to math, science, and coding hints that higher-level reasoning abilities may not easily generalize to other areas. Timothy Lee notes:

While o1 represents a significant improvement in reasoning about math and science, the o1 models are not “truly general” in their reasoning abilities. For example, they are not noticeably better than other frontier models at reasoning about language. I suspect this is because the OpenAI team hasn’t figured out an automated way to generate the kind of training data they would need to do reinforcement learning on language tasks.

We can’t yet guess at how difficult it will be to extend the techniques used in AlphaProof and o1 into new fields, especially those that don’t have clear right and wrong answers. Nor do we know what will be required to address real-world problems that, unlike math puzzles, require lots of messy context. Along the way, we will likely encounter new challenges – something other than just extending the reasoning chain, some gap in LLM capabilities that’s difficult to put a finger on today. Again, if AI capabilities were just a question of scale, then OpenAI wouldn’t have had to create o1 in the first place. Sam Altman again:

There was a time in our history when the right thing to do was just to scale up compute. Right now the answer is to really push on research - o1 was a giant research breakthrough that we were attacking on many vectors for a long time.

Creativity is an exploratory process, requiring a diverse set of strategies. Employing those strategies requires developing muscle memory for each problem domain. AlphaProof and o1 demonstrate a path forward, but the need for large amounts of training data, and open questions around how to create that data for messy tasks, suggests that progress will be uneven, gradual, and idiosyncratic.

Thanks to Dynomight, Grant Mulligan, Julius Simonelli, Kevin Kohler, Quade MacDonald, Rob Tracinski, Sean Fleming, and Shreeda Segan for invaluable feedback and suggestions.

1. Large Language Models, like the GPT-4o model that powers ChatGPT

2. Prior to the recently introduced “o1” model, at any rate.

3. Note that when I refer to “current LLMs”, I am excluding the new AlphaProof and o1 models. Arguably, these are not strictly language models, because they don’t just predict the next token in standard written language; I’ve seen o1 referred to as a “Large Reasoning Model”.

4. These training proofs are apparently generated by AlphaProof itself. It bootstraps its own learning in a similar fashion to DeepMind’s AlphaZero (chess) and AlphaGo Zero (Go).

5. Problem 1 from the 2024 International Mathematical Olympiad:

6. I’m not quite clear on how generating several hundred guesses and then looking for counterexamples fits into a tree search over potential proofs, so my understanding of how AlphaProof works may be flawed.

7. From https://openai.com/index/learning-to-reason-with-llms/

8. To decode: Convert each letter to a number: a=1, b=2, etc. Take the numbers two at a time, average them, and convert back to a letter. For instance, the first two letters (“oy”) decode to “t”, because o=15, t=25, the average is 20, and t=20. The result: “THERE ARE THREE R’S IN STRAWBERRY”. (This is a reference to the notorious fact that current LLMs incorrectly answer “how many r’s in strawberry”.)

9. I asked:

Please solve the following math puzzle. You are given the numbers 2, 3, 7, 20, 21, 25. You need to find some way of combining those numbers using addition, subtraction, multiplication, and division to make 269, using exactly three operations. You cannot use the same number twice. For example, (3 * 7) + 20 would make 41. Can you find a way to make 269?

This puzzle is not especially difficult, but o1-preview flubbed it. After thinking for 67 seconds, it came up with the following:

Final Answer: (21 × (20 − 7)) − (25 − 21) = 269

So, by performing these three operations using the given numbers without repeating any number, we successfully arrive at 269.

The arithmetic is correct, but while it claims to have used three operations (as requested), it actually used four. And, contrary to the instructions, it used a number (21) twice. When I pointed this out, it thought for another 82 seconds, and then claimed that no solution exists.

(The solution I arrived at after working on the problem in my head for a minute or so: 2 * 7 * 21 - 25 = 269.)

10. Here is an assortment of additional observations on o1’s performance.

The paper LLMs Still Can’t Plan; Can LRMs? A Preliminary Evaluation of OpenAI’s o1 on PlanBench reports on o1’s performance on “Blocksworld”, a set of puzzles which require rearranging blocks. On a set of puzzles requiring 2 to 16 steps, o1 scores 97.8%, a huge advance over the best previous LLM result (62.6%). However, on larger puzzles requiring 20 to 40 steps, “o1-preview only manages 23.63%, and most of this accuracy comes from correctly solving problems which require fewer than 28 steps. While these models are overall impressive, this shows that their performance is still far from robust.”

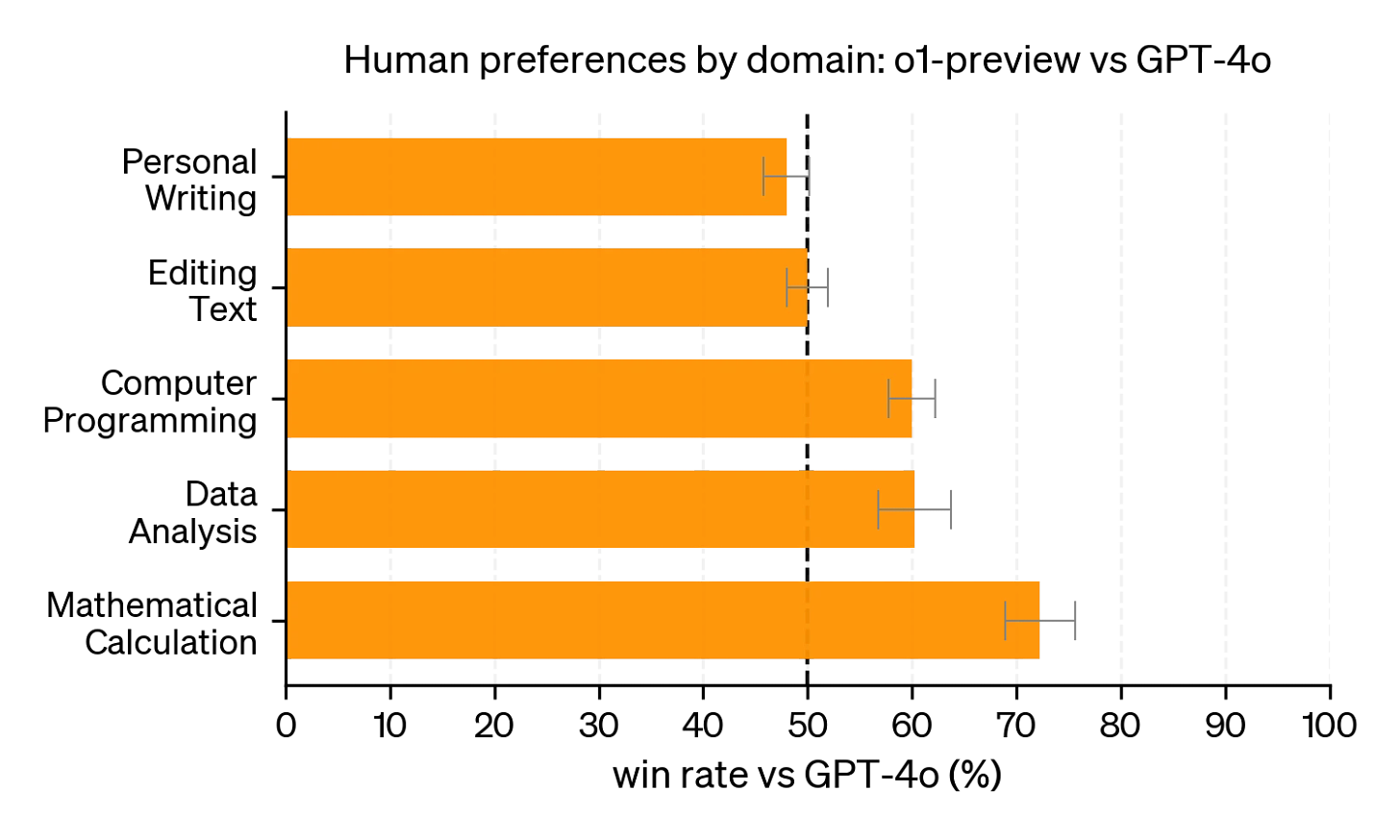
OpenAI’s own tests show that o1-preview’s results, when judged by human evaluators, are slightly worse than GPT-4o for “personal writing”, and only comparable for “editing text”:

Via Zvi:

Anthony Aguirre: I've subsequently been feeding it some pretty challenging mechanics problems. It got one perfectly, one with a single hint/step in thinking corrected, and nearly succeeded in a third (correctly doing a hard calculus of variations problem but not being able to construct the tricky argument to pull things together. Note that I think it would have gotten this were the solution in its training data.)

I would not give these problems in a graduate qualification exam because they are too hard. My sense so far is that it lacks a certain inventiveness and ability to take intuitive leaps, but it absolutely can carry out long hard physics calculations reliably toward a correct solution; I'd wager that it would pass the physics quals at most or all physics graduate programs.

Brian Chau notes (thanks to Zvi for the link):

TLDR: Based on my testing on national-level Math Olympiad and Programming Olympiad questions, o1 appears to be:

a) the greatest lookup/citation system in existence, blowing away perplexity

b) still mediocre at solving problems that aren't direct applications of documented theorems

11. More precisely, gpt-4o.

12. Search for “Chain of Thought”, click on a topic (“Cipher”, “Coding”, etc.), scroll down under “OpenAI o1-preview”, and click “Thought for 5 seconds”.

13.  Rohan Paul shares some thoughts, noting a paper from OpenAI which mentions training on “800K human-labeled solution steps”. The paper was published in May 2023, and may reflect work done earlier, so o1’s training data could have been much larger.

14. GPT-4o can generate about 100 tokens per second. If o1 is similar, then over the course of 24 hours it would generate 8.64 million tokens, which would be a very large token buffer. To allow an AI to chew on a problem for an entire day will require new approaches to information management.

15. At OpenAI’s recent DevDay event; paraphrased by Simon Willison.